Scisnack | Stable water isotopes: a powerful – but often overlooked

Stable water isotopes (SWIs) have been used in meteorology since the 1950s, but they continue to be an underutilised resource in the meteorologist’s toolbox. Not all water molecules are created equal in that they differ by how much they weigh and how rare they are. However, they are all embedded in the same humidity that meteorologists all around the world observe. And they have the potential to serve as a much needed check of the water cycle in weather forecasting models, highlighting sources of errors.

First, some basic background on SWIs; all varieties of water molecules are composed of two atoms of hydrogen (H) and one atom of oxygen (O). In the most abundant variety, the hydrogen atoms have one proton and no neutrons, while the oxygen has eight protons and eight neutrons, and is denoted with the formula of H₂¹⁶O. This SWI accounts for around 99.8% of all water. The remaining 0.2% is mostly made up by the other three varieties: H²H¹⁶O (HD¹⁶O), H₂¹⁷O, and H₂¹⁸O. In HD¹⁶O, one of the hydrogen atoms has a neutron, and is twice as massive as ordinary hydrogen. This isotope of hydrogen even has its own name, deuterium (D). The other two SWIs involve the oxygen atom, adding one and two neutrons, respectively. On a practical level, they are indistinguishable from one another, in that all of them behave as one would expect water to behave. However at the molecular level, their differences become apparent.

The fundamental difference between the varieties is mass, and with differences in mass, comes differences in motion. Everything above absolute zero (-273.15 ℃) moves on the molecular level. And since temperature is the average kinetic energy of the molecules, momentum dictates that the different SWIs will have marginally different speeds, with the heavier SWIs being slightly slower than the lighter. For example, HD¹⁶O moves faster than H₂¹⁸O, but slower than H₂¹⁶O. These differences of speed become really important during phase transition (such as evaporation), since the molecules are moving from one reservoir to the other, which gives the opportunity for the ratio in each reservoir to change.

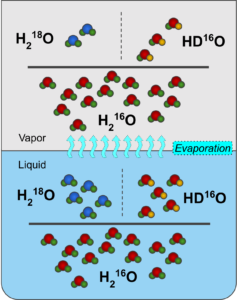
This change in ratio is so important, that it even has its own term: fractionation. Heavier molecules have a tendency to stay in lower energy states (e.g. a liquid is a lower energy state as compared to a gas). Then during a phase change such as evaporation, the lighter H₂¹⁶O will more readily transition to the vapor phase as compared to the heavier H₂¹⁸O. As such, the higher energy state will have a relatively smaller abundance of heavy isotopes (the vapor would be considered “depleted”). The SWIs have undergone isotopic fractionation, and it is the reason why SWIs are so useful in meteorology.

Phase changes like evaporation don’t just abruptly occur at set temperatures, such as what we might practically experience with the boiling point of water at 100 ℃. Like rain puddles disappearing in the sun, evaporation can happen below this threshold. How much fractionation occurs during evaporation is dependent on the temperature of the liquid water. We can quantify this with a coefficient called the fractionation factor. So because the fractionation factor is related to the temperature, measuring and knowing the ratio of heavy to light isotopes in both the vapor and the liquid, we can find out what the temperature of the evaporating water was.

Thinking and working in relative ratios is fine for an independent theoretical approach, but comparisons between studies require a less relativistic framework. For this purpose, we can introduce a standard against which all relative ratios can be compared. For SWIs, this is the V-SMOW (Vienna Standard Mean Ocean Water), which has defined relative ratios of heavy to light isotopes. Differences between this standard and a given water sample are usually small and are expressed in permille (per thousand, ‰). This notation is denoted with a leading delta (δ) in front of the defining isotope. So V-SMOW has δD, δ¹⁷O, and δ¹⁸O equal to 0 ‰. Now, if we assume our evaporating water is a very, very large reservoir of V-SMOW (aka the global oceans), we only have to measure the vapor to work out the temperature of the water, since our evaporating water is the zero standard. Of course, in the “real world” there are other influences to consider, but measuring the water vapor is where it starts, which is commonplace in meteorology. And thanks to advances in technology, it’s getting a lot easier to measure the SWIs in that vapor.

Using laser-based spectrometers, we can make in-situ measurements of SWIs at unprecedented temporal resolution. We are able to discern information on the history of the phase transitions undergone by the water by simply studying the SWIs at the measurement site. We can also study individual processes taking place in the atmospheric water cycle. This is all towards the goal of bettering the representation of the water cycle in numerical weather and climate models, by using the SWI cycle as a constraint. This cycle would act like a balance, making sure that the amount of water wouldn’t just sum up to the correct value in the end, but that the processes driving the water cycle wouldn’t be compensating against each other. And as SWI measurement technology continues to advance, hopefully the SWI toolbox will become more accessible to meteorologists around the world.