In the petroleum industry, we use exploration seismology to obtain some properties of rocks below our feet. We artificially generate vibrations at a source point on the ground to emit seismic waves underground. Different rock interfaces reflect seismic waves back to the surface. Detectors on the ground receive this reflected wave and record it as seismic data. The seismic data carries information about the physical properties of the rock, such as velocity and density.
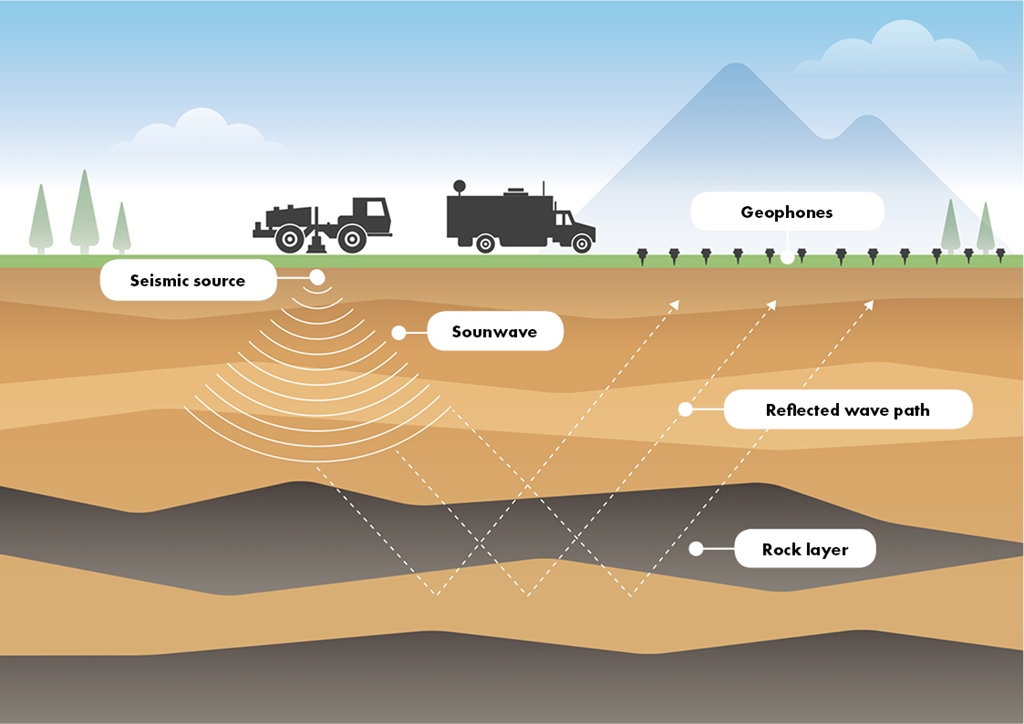
An example of seismic exploration. Image source: Energy Information Australia.
In order to transfer seismic data into rock properties, we first have to find the mathematical relationship between them. There are many physical equations describing this relationship, such as wave equations and Helmholtz equations. Usually, we use Helmholtz equations, which look like this:
![\[\left( \nabla \cdot \frac{1}{\rho}\nabla + \frac{\omega^2}{\rho v^2} \right)P = -S,\]](https://www.scisnack.com/wp-content/ql-cache/quicklatex.com-ea892ee2c2c92aede705c4a1b54283da_l3.png "Rendered by QuickLaTeX.com")
where ρ is the density, v is the velocity, ω is the frequency, ∇ is the differential operator, P is seismic data observed on the surface and S is the source term that describes the artificially generated vibration.
This equation contains the differential operator, and therefore we need to use an iterative algorithm to solve it. First, we set up an initial subsurface rock model. Then we use the Helmholtz equation to obtain the synthetic seismic data generated by the initial model. Next, we get the difference between the synthetic seismic data and the observed seismic data. By relating this difference to rock properties, we can modify our rock parameters to minimize the difference and eventually obtain an improved subsurface model. Further, we use the modified model as initial model and repeat the above steps until the difference is iterative-tuned to a minimum. Finally, we can use our iterative-tuned model to obtain the actual rock properties from seismic data.
Geophysicists have proved that this iterative-tuning method is an effective means to establish an accurate model for rock properties. Some numerical experiments validate that this method can obtain rock parameters that are almost the same as real subsurface model.
This method seems to be perfect. However, we use it with assumptions about the initial model and the source. First, we need a good initial model to make sure the iterative result is correct. However, in the case of complex geology, obtaining the correct initial model is very difficult. Secondly, the source term is hard to describe the practical source vibration. In addition, this method needs to synthesize seismic data when we need to modify the rock properties, resulting in a huge amount of computation.
We can obtain the information of rock below our feet from seismic data through the geophysical method. Nevertheless, the challenges remain, and we will continue to improve this method using some other mathematical algorithms.
0
0
0
0
0
0
Kui Xiang
Latest posts by Kui Xiang (see all)
- What seismic data tell us about rocks below our feet - October 23, 2019