The Century Problem – An Unsolved Puzzle in Meteorology

Date
Comments: 2 Comments

For about 75 years, many brilliant minds all over the world have struggled to find a unique solution: one that limits flood-caused damages; a solution that allows the prediction of flash-floods, rainfall caused avalanches and slides; and one that will help thousands of people to survive each year. The way out of the dilemma is to find a correct relation between rainfall and radar reflectivity. However, it is still the most famous, unsolved struggle in radar meteorology.

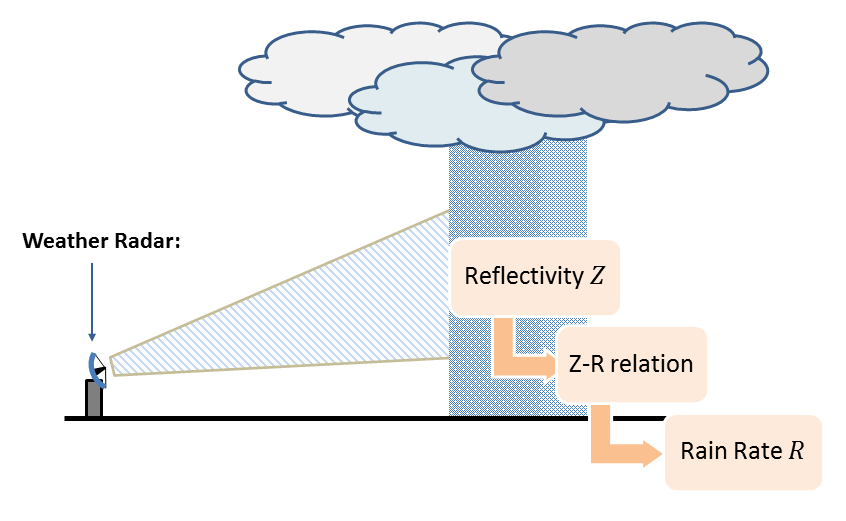
Conversion of the measured reflectivity Z into a quantitative rain amount R © Lucas Höppler

Conversion of the measured reflectivity Z into a quantitative rain amount R. © Lucas Höppler

 

A radar sends out a pulse of energy and only measures the backscattered reflectivity. The Z-R relation is an equation which converts the measured unusable reflectivity Z into a quantitative rainfall amount R.

It sounds theoretical and rather complicated (and in fact, it’s both), but it is essential for the development of reliable flash-flood warning systems. If the Z-R relation is wrong, either nothing happens and people are wrongly warned, or they are taken by surprise by a rapid moving, devastating wave of muddy water and die. Z-R relations are important, but until now, no effective solution exists to convert the reflectivity to an accurate rain amount.

So what are some of the problems to address?

The first problem is a mathematical one and, sadly, non-fixable. The reflectivity Z is a quantity that depends on the sixth power of the rain drop size diameter. The rain amount R is a quantity that depends on the third power of the rain drop size diameter. For mathematicians this is a clear case: There is no analytical equation connecting the two quantities Z and R as long as the raindrop size distribution is not known. And, the raindrop size distribution is highly variable from rain event to rain event. Therefore, most authors use an empirical power function with the form Z=aRb to calculate the rain amount from the measured reflectivity.

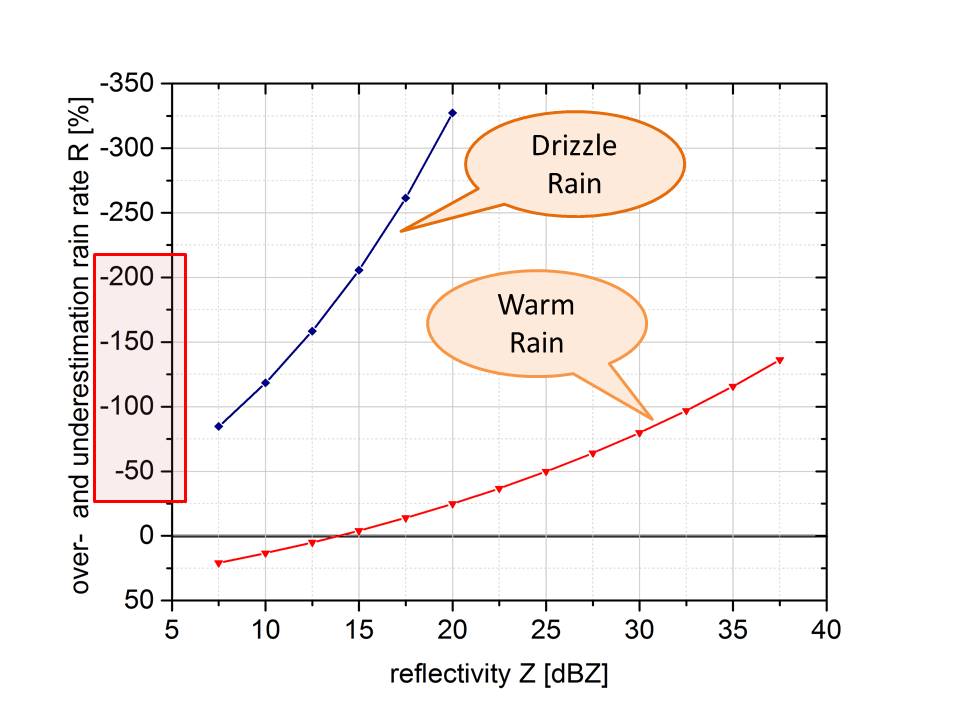
Over- and underestimation of the rain rate if the Marshall & Palmer Z-R relation is used, although the Z-R relation for drizzle rain or the Z-R relation for warm rain of Bergen, Norway is valid. © Lucas Höppler

Over- and underestimation of rain rate if the Marshall & Palmer Z-R relation is used, although the Z-R relation for drizzle rain or the Z-R relation for warm rain of Bergen, Norway is valid.
© Lucas Höppler

 

The second one is that we only have the one equation Z=aRb with two unknowns a and b. Through experiments it is possible to determine the coefficients a and b. Marshall & Palmer (1948) found the relation Z=200R1.6 with the parameters a=200 and b=1.6, which is widely used, among others, also by the Meteorological Office in Norway (MET.no).

The third problem – and it matters now – is that the parameters a and b are used operationally as constants, but actually vary strongly from one rain event to another. Within one hour, the parameter a can easily vary between 100 and 300. And in fact, the parameters depend on atmospheric conditions, on the geographic locality, and on the rain type. A wrong parameter a, and the calculated rain rate is 200 % higher or lower than it actually should be.

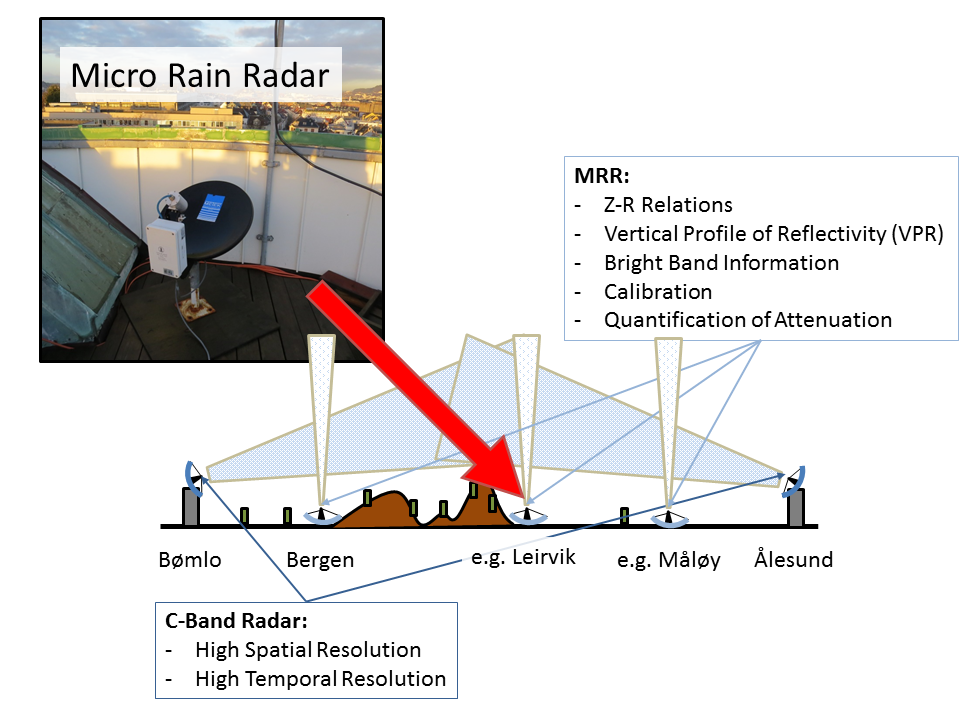
Use Micro Rain Radars to support operational weather radars!
© Lucas Höppler

 

 

A so called Micro Rain Radar (MRR) can provide a solution to the still unsolved Z-R problem, since it provides Z-R relations in nearly real-time. If you ask me, to solve the Z-R problem, two or three Micro Rain Radars for every operational weather radar are the way to go. With these real-time radars, the hydrological models receive the necessary input. As a result, flood or flash-flood forecasting will be improved. The geographical position of hydropower plants can be optimized. Buildings and roads could be made flood resistant. All these benefits are given by operating some supportive Micro Rain Radars.

In 2015, Norway lost about 51 Million Euros because of flood damages and not less in the previous years (NASK – Norsk Naturskadepool).

 
Could this problem be avoided in the future with Micro Rain Radars?


Absolutely.

References:
Marshall, J. S., and W. McK. Palmer 1948. The distribution of raindrops with size. J. Meteor.. 5. 165–166.

Share on Facebook0Tweet about this on TwitterShare on LinkedIn0Share on Tumblr0Share on Google+0Pin on Pinterest0Share on Reddit0

Lucas Höppler

Lucas writes currently his master's thesis at the University of Bergen (UiB), Norway in collaboration with the Ludwig Maximilians University of Munich, Germany under supervision of Prof. Joachim Reuder (UiB) and Dr. Martin Hagen (German Aerospace Center, DLR). His focus lies on weather radar technology and the development of new methods to increase the accuracy of rainfall measurements.
SciSnack Disclaimer: We write in SciSnack to improve our skills in the art of scientific communication. We therefore welcome comments concerning the clarity, focus, language, structure and flow of our articles. We only accept constructive feedback. All comments are manually approved and anything slightly nasty will not be accepted.